将棋AIで学ぶディープラーニング on Mac and Google Colab

AI
2024.04.10

[モンテカルロ木探索]
第12章 詳細

ハッシュ

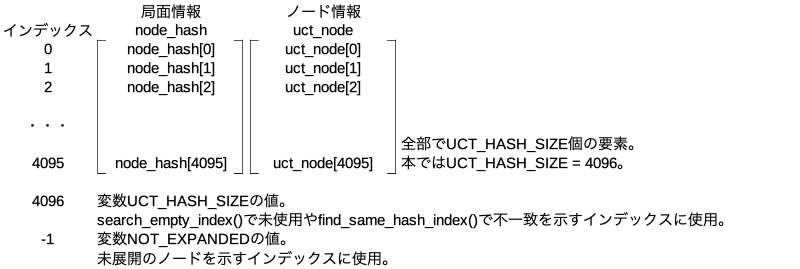
ハッシュとは局面を数字に置き換えたもの。node_hashの中にハッシュが入っている。局面とノード情報を紐づけていろいろ処理する目的で使う。

インデックス

0から始まる整数で全部でUCT_HASH_SIZE個。本では4096個。ハッシュの値をhash_to_index()という関数に入力してインデックスに変換し、そのハッシュの値とインデックスを紐づけて使う。ハッシュの数値をそのままインデックスとして使わずに一旦4096の幅にする理由はハッシュのサイズが64bitと無駄に大きいため。

node_hash

node_hashは配列。要素1個1個はNodeHashEntryクラスのインスタンスでそれぞれの要素がハッシュ、手番、手数、フラグの情報を持つ。生成するときはself.xxx = NodeHash()でまずNodeHashクラスのインスタンスを生成する。このxxxというインスタンスの中にnode_hash配列がメンバとして存在する。

本ではxxxにnode_hashという名前を付けており中の配列と同じ名前になっている。混乱しそうなので注意。

node_hashを少し詳しく見てみる

骨子だけ抜き出すとこうなる。

UCT_HASH_SIZE = 4 # 2のn乗であること。本では4096。説明用に4とした。

class NodeHashEntry:
    def __init__(self):
        self.hash = 1     # ゾブリストハッシュの値。本当は0。説明用に1とした。
        self.color = 2    # 手番。本当は0。説明用に2とした。
        # self.moves = 0    # 説明簡略化のため省略。
        # self.flag = False # 説明簡略化のため省略。

class NodeHash:
    def __init__(self):
        self.node_hash = [NodeHashEntry() for _ in range(UCT_HASH_SIZE)]

構造を理解するためにいろいろやってみる。まず、クラスNodeHashのインスタンスaを作成してprintしてみる。

a = NodeHash()
print(a)

返答

<__main__.NodeHash object at 0x0000015BDBB54948>

このクラスはnode_hashという変数名の配列を持っており、今回の場合だとUCT_HASH_SIZE ＝ 4なのでこの配列の要素数は4個である。
node_hash = [NodeHashEntryオブジェクト, NodeHashEntryオブジェクト,
NodeHashEntryオブジェクト, NodeHashEntryオブジェクト]。

aのnode_hash配列をprint

print(a.node_hash)

返答

[<__main__.NodeHashEntry object at 0x0000015BE2B7FD88>, 
<__main__.NodeHashEntry object at 0x0000015BE4E13E48>, 
<__main__.NodeHashEntry object at 0x0000015BE67F0108>, 
<__main__.NodeHashEntry object at 0x0000015BE65B5F08>]

この4個のオブジェクトはそれぞれhashとcolorという変数を持つ。

4個のオブジェクトのhashとcolorをprint

for i in range(4):
    print(a.node_hash[i].hash, a.node_hash[i].color)

返答

1 2
1 2
1 2
1 2

uct_node

uct_nodeは配列。要素1個1個はUctNodeクラスのインスタンスでそれぞれの要素がノードの訪問回数、勝率の合計、子ノードの数、子ノードの指し手、子ノードのインデックス、子ノードの訪問回数、子ノードの勝率の合計、方策ネットワークの予測勝率、価値ネットワークの予測勝率、評価済みフラグの情報を持つ。生成するときはself.uct_node = [UctNode() for _ in range(UCT_HASH_SIZE)]で生成する。

search_empty_index()

未使用のインデックスを探すメソッド。引数はハッシュ、手番、手数。

やっていることは、ハッシュからインデックスを生成しnode_hash配列のそのインデックスの要素が未使用かどうか調べる。未使用だったら引数のハッシュ、手番、手数をその要素に代入し、その要素が使用済みであることを示すフラグを立てる。使用済みだったらインデックスを1加算しながら全インデックスを1周するまで同じことを行う。1周して未使用のインデックスが無かったらUCT_HASH_SIZEを返す。

例えばUCT_HASH_SIZE = 4096で、未使用のインデックスが有る場合はnode_hash[0]〜node_hash[4095]の4096個の中の最初にヒットした要素にハッシュ、手番、手数を代入しフラグを立てて終了。未使用のインデックスが無い場合は4096という値を返して終了。

find_same_hash_index()

局面に対応するインデックスを探すメソッド。引数はハッシュ、手番、手数。

やっていることは、ハッシュからインデックスを生成しnode_hash配列のそのインデックスの要素が未使用かどうか調べる。未使用だったらUCT_HASH_SIZEを返す。使用中でその要素のハッシュ、手番、手数が引数と一致したらそのインデックスを返す。インデックスを1加算しながら全インデックスを1周するまで同じことを行う。1周して引数と一致するインデックスが無かったらUCT_HASH_SIZEを返す。

例えばUCT_HASH_SIZE = 4096で、引数のハッシュ、手番、手数と一致する要素が有る場合はその要素のインデックス（0〜4095の4096個の中のどれかになる）を返して終了。一致する要素が無い場合は4096という値を返して終了。

search_empty_index()もfind_same_hash_index()もnode_hash配列と同じインスタンスの中に存在する。よって使うときはself.インスタンス名.search_empty_index()とすれば良い。本ではインスタンス名がnode_hashとなっておりメンバ配列のnode_hashと同じ名前で混乱しそうなので注意。

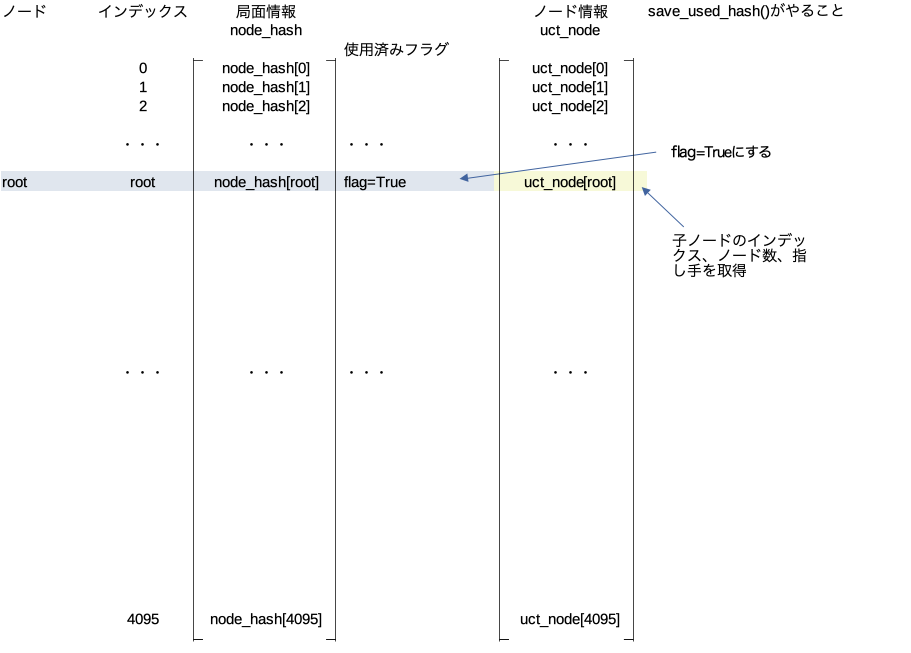
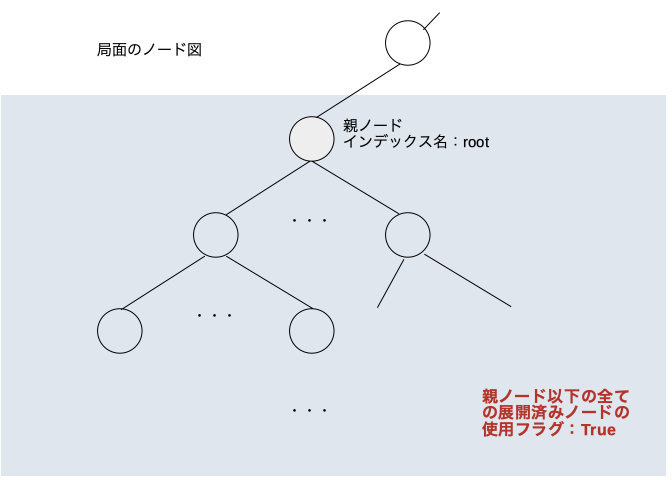
save_used_hash()

この関数が行う処理は引数に与えたノード以下の全ての展開済みノードに対して使用済みフラグを立てるという処理。

    # 使用中のノードを残す
    def save_used_hash(self, board, uct_node, index):
        self.node_hash[index].flag = True
        self.used += 1

        current_node = uct_node[index]
        child_index = current_node.child_index
        child_move = current_node.child_move
        child_num = current_node.child_num
        for i in range(child_num):
            if child_index[i] != NOT_EXPANDED and self.node_hash[child_index[i]].flag == False:
                board.push(child_move[i])
                self.save_used_hash(board, uct_node, child_index[i])
                board.pop()

最初の処理

引数に与えたノードの使用済みフラグを立てる。子ノードに元々入っていた情報はまた使えるようになる。

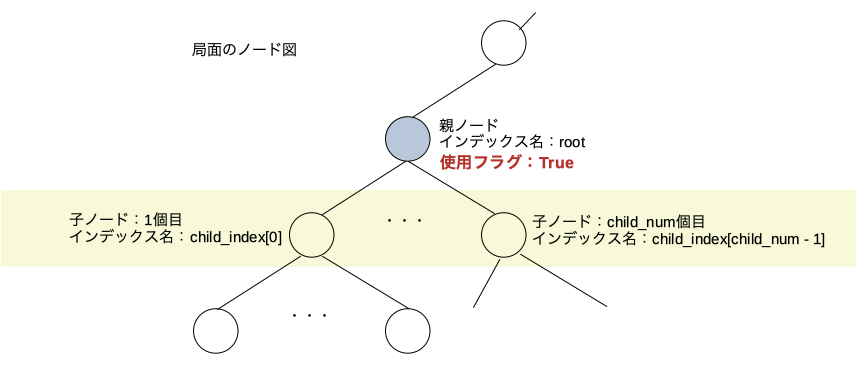
次の処理

子ノードの使用済みフラグを立てる。子ノードに元々入っていた情報はまた使えるようになる。

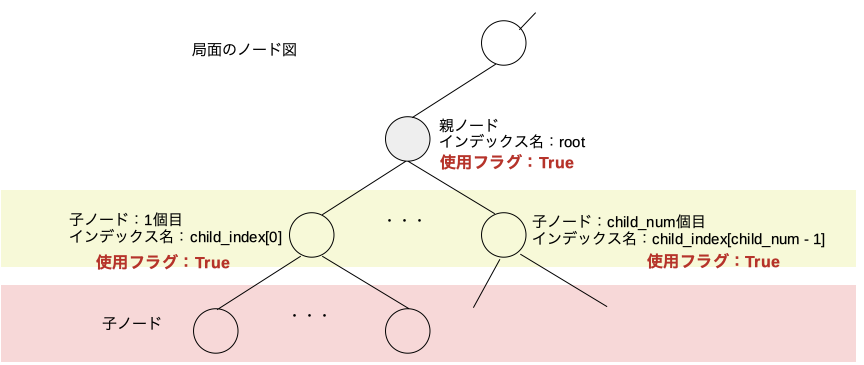
最終的に

これを繰り返していく。そうすると最終的に親ノード以下の全ての展開済みノードの使用済みフラグが立ち元々入っていた情報はまた使えるようになる。

delete_old_hash()

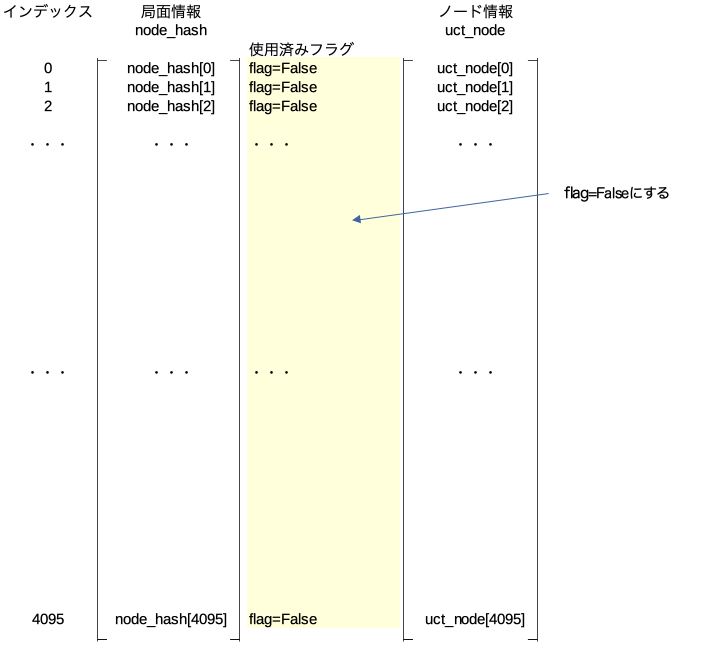
この関数が行う処理は引数に与えられた局面のノード以下の全ての展開済みノードの使用済みフラグを立て、その他のノードは不使用のフラグを立てるという処理。

最初の処理

全てのnode_hashに対して使用済みフラグをFalse（不使用）にする。

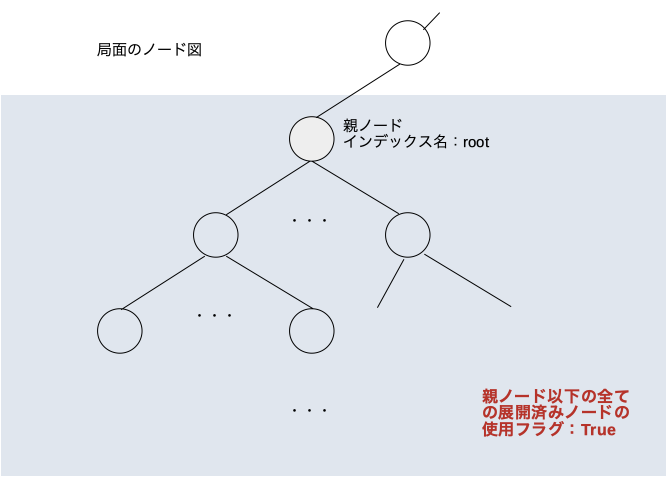
最終的に

現局面に対してsave_used_hash()を実行する。現局面ノード以下の全ての展開済みノードの使用済みフラグが立ち元々入っていた情報はまた使えるようになる。

expand_node()

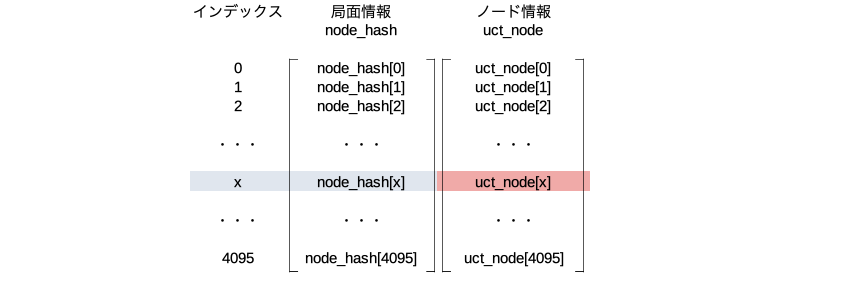
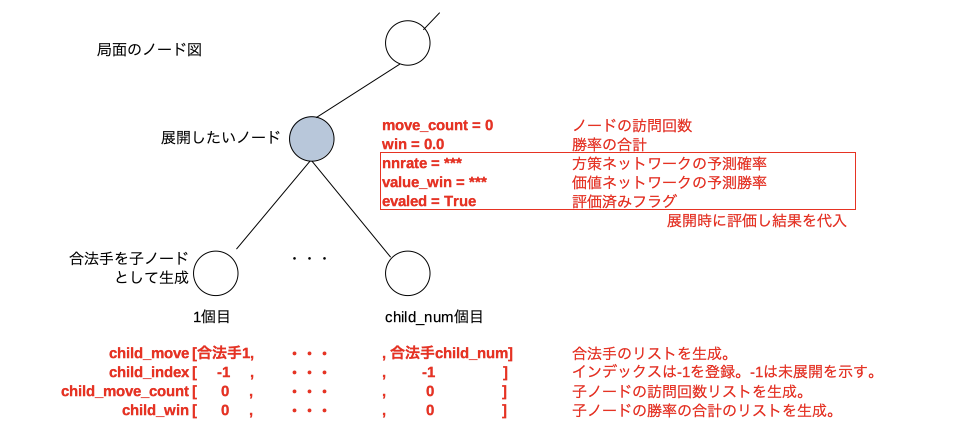
未展開のノードを展開するメソッド。例えば下図のような展開したいノードが有ったとする。

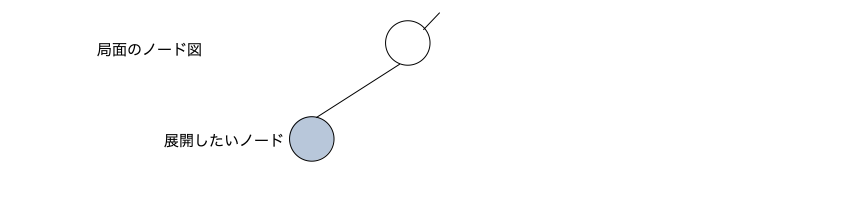
node_expand()を行うと、そのノードのハッシュからインデックス（ここではxとする）を決めてnode_hash[x]とuct_node[x]をこのノード用に割り当てる。赤文字部分に示す9個のパラメータを生成しuct_node[x]のメンバ変数として保存する。

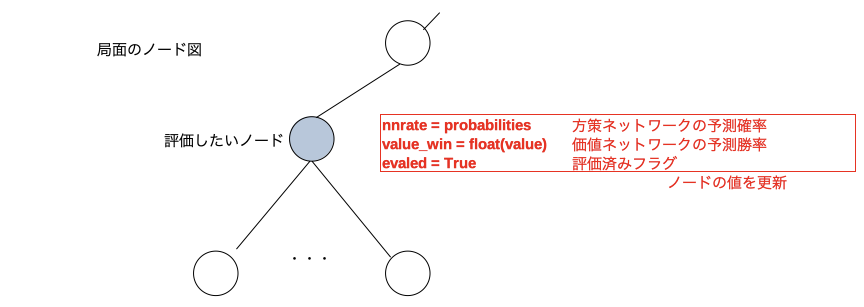
eval_node()

評価したいノードの局面を入力とし方策ネットワークの予測確率と価値ネットワークの予測勝率を出力するメソッド。例えば下図のような評価したいノードが有ったとする。

局面情報をニューラルネットワークに入力して方策ネットワークの予測確率と価値ネットワークの予測勝率を得る。

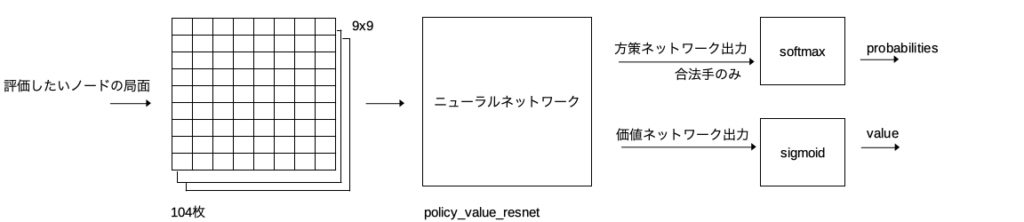
ノード情報（赤文字の3つ）を更新する。

select_max_ucb_child()

4章に出てきた以下の式の値いわゆるUCB値が最大となる子ノードを選択するメソッド。

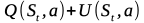
image.png

Stは現在のノードの状態、つまり局面のこと。
aは候補手。
Q(St,a)は期待値項。状態Stにおける行動aの行動価値を表す。本では子ノードaの合計勝率を子ノードaの訪問回数で割った値としている。
U(St,a)はボーナス項。探索回数が少ない手ほど優先して選択される。さらに方策ネットワークで得た指し手の確率P(s,a)も利用して有望な手が優先して探索されるようにする。

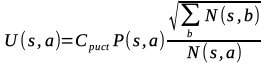
image.png

Cpuct : ボーナス項の重みを調整する定数。
P(s,a) : 方策ネットワークの予測した着手確率。
N(s,a) : 状態sにおける行動aの訪問回数。本では+1している。訪問回数0のときに分母が0になるのを避けるためか。
√ΣN(s,b) : 状態sにおけるすべての行動の訪問回数。

実際select_max_ucb_child()でやっていることのイメージ図

前へ次へ
1234567891011121314151617181920

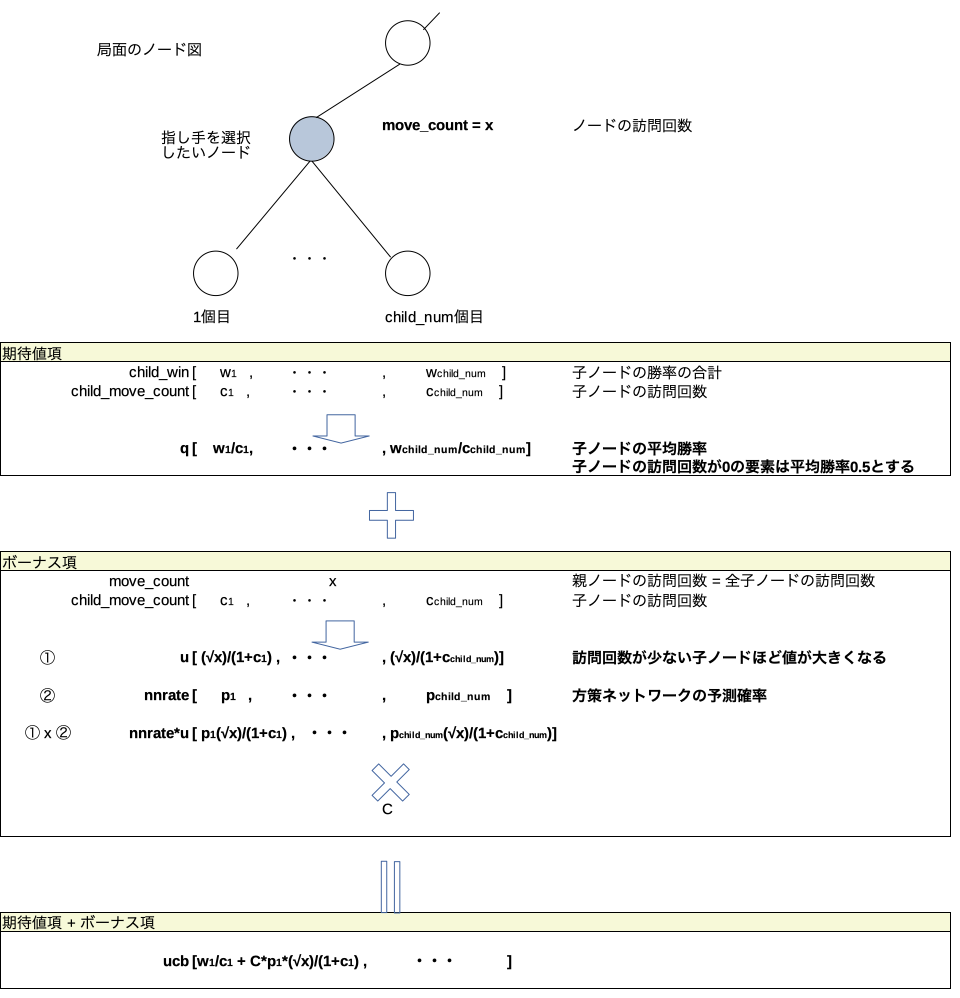
コメント

タイトルとURLをコピーしました